Jayfeather9's Blog
0%

数学建模国赛算法整理-1

Posted on Edited on In Views:
一份不完整的简单普通的数学建模国赛算法整理。

大略总结

不一定后文有对应详细解释

https://zhuanlan.zhihu.com/p/647440460

机理分析类：来源于实际问题，需要了解一定的物理机理，转化为优化问题。
微分方程模型、数值模拟等

优化类：纯优化问题，旨在找到使某个目标函数取得最大或最小值的最优解,对于机理要求要求不高，重在求解。
线性规划：内点法、单纯形法、修正单纯形法、
非线性规划：下山单纯形法、改进的BFGS拟牛顿法、改进的共轭方向法、（边界）截断牛顿法、线性近似束优化方法、序贯最小二乘规划算法、信赖域算法、
整数规划：分支定界法、0-1规划、枚举法、
启发式算法：遗传算法（GA）、粒子群算法（PSO）、模拟退火算法（SA）、蒙特卡洛

评价类：纯评价问题，通过构建合适的指标和评价方法，评价模型能够对不同方案的优劣进行比较和分析。
层次分析法、因子分析（探索性）、数据包络分析(DEA)、模糊综合评价、优劣解距离法(TOPSIS)、秩和比综合评价法(RSR)、耦合协调度、熵值法、CRITIC权重法、独立性权系数法、变异系数法、灰色关联分析、多准则妥协解排序法(VIKOR)、解释结构模型(ISM)

数理统计模型（主要是预测类）：数理统计模型可以通过对给定数据集的统计分析，推断出数据的分布规律、相关性、假设检验等，为问题提供支持和解决方案。
arima、机器学习、灰色预测、问卷分析、相关分析、差异分析等等

={aaabbbccc=\left\{\begin{aligned}aaa\\bbb\\ccc\end{aligned}\right.

前/后向欧拉法

由泰勒展开：

f(x+Δx)=f(x)+f′(x)Δx+f′′(x)(Δx)22!+O(Δx)2\begin{aligned}f(x+\Delta x)=f(x)+f'(x)\Delta x+\frac{f''(x)(\Delta x)^2}{2!}+O(\Delta x)^2\end{aligned}

f(x−Δx)=f(x)−f′(x)Δx+f′′(x)(Δx)22!+O(Δx)2\begin{aligned}f(x-\Delta x)=f(x)-f'(x)\Delta x+\frac{f''(x)(\Delta x)^2}{2!}+O(\Delta x)^2\end{aligned}

可得函数导数一阶近似：

f′(x)=f(x+Δx)−f(x)Δx+O(Δx)\begin{aligned}f'(x)=\frac{f(x+\Delta x)-f(x)}{\Delta x}+O(\Delta x)\end{aligned}

=f(x)−f(x−Δx)Δx+O(Δx)\begin{aligned}=\frac{f(x)-f(x-\Delta x)}{\Delta x}+O(\Delta x)\end{aligned}

分别为前向和后向展开。如果将泰勒展开两式相减可得二阶近似：

f′(x)=f(x+Δx)−f(x−Δx)2Δx+O(Δx)2\begin{aligned}f'(x)=\frac{f(x+\Delta x)-f(x-\Delta x)}{2\Delta x}+O(\Delta x)^2\end{aligned}

类似的，对于二阶导数，可以导出：

f′′(x)=f(x+Δx)−2f(x)+f(x−Δx)(Δx)2+O(Δx)2\begin{aligned}f''(x)=\frac{f(x+\Delta x)-2f(x)+f(x-\Delta x)}{(\Delta x)^2}+O(\Delta x)^2\end{aligned}

相应的离散化可能出现两种误差：截断误差和舍入误差，分别对应前述离散化未计算高阶导数项的误差和计算机浮点数计算的误差。

显式求解时对于方程 ∂f∂t=∂2f∂x2\begin{aligned}\frac{\partial f}{\partial t}=\frac{\partial^2 f}{\partial x^2}\end{aligned} 离散化得到：fin+1−finΔt=fi+1n−2fin+fi+1n(Δx)2\begin{aligned}\frac{f^{n+1}_i-f^n_i}{\Delta t}=\frac{f^n_{i+1}-2f^n_i+f^n_{i+1}}{(\Delta x)^2}\end{aligned}

其中 finf^n_i 代表方程离散化后时间为 nΔtn\Delta t，空间为 iΔxi\Delta x 的值。

前述方程可重排列得到：fin+1=fin+Δt(Δx)2(fi+1n−2fin+fi−1n)\begin{aligned}f^{n+1}_i=f^n_i+\frac{\Delta t}{(\Delta x)^2}(f^n_{i+1}-2f^n_i+f^n_{i-1})\end{aligned}

稳定条件为：Δt(Δx)2≤12\begin{aligned}\frac{\Delta t}{(\Delta x)^2}\le \frac{1}{2}\end{aligned}

最小二乘法

2020-A070

{1×k+b=20×k+b=22×k+b=3\left\{ \begin{aligned} 1\times k + b = 2 \\ 0\times k + b = 2 \\ 2\times k + b = 3 \\ \end{aligned} \right.

像这样的一个问题，就是有一个线的方程 kx+b=ykx+b=y 要求过三个点 (1,2),(0,2),(2,3)(1,2),(0,2),(2,3)，就将其代入后整理成向量乘法形式：

[102]×x1+[111]×x2=[223] \left[ \begin{aligned} 1 \\ 0 \\ 2 \\ \end{aligned} \right] \times x_1 + \left[ \begin{aligned} 1 \\ 1 \\ 1 \\ \end{aligned} \right] \times x_2 = \left[ \begin{aligned} 2 \\ 2 \\ 3 \\ \end{aligned} \right]

这样我们就可以对方程组进行求解。但是显然这个方程是无解的，因为前两个向量构成的平面上没有第三个向量，但我们可以把第三个向量投影到前两个向量的平面上，组成一个最接近我们需要的解答的近似解。

类似这样就是最小二乘法的思想了。

数学上通用的求解方法描述如下：

对于函数 hθ(x1,x2,...xn)=θ0+θ1x1+⋯+θnxnh_\theta(x_1,x_2,...x_n)=\theta_0+\theta_1x_1+\dots+\theta_n x_n ，其可以表示为矩阵形式：

hθ(x)=Xθ=Yh_\theta(\bold x)=\bold X\theta=\bold Y

其中 X\bold X 为 m×nm\times n 的矩阵，代表有 mm 个样本数据，希望求解出一个合适的函数 hh 满足这些样本， nn 为样本特征数。

经计算可得，θ=(XTX)−1XTY\theta=(\bold X^T\bold X)^{-1}\bold X^T\bold Y

适用于对于一组样本和对应的输出，求满足其变化规律的函数。注意特征数太高可能会造成过拟合，需要加入正则化项。同时由于要进行矩阵求逆，运算量可能较大。

有限元差分

2020-A070
2020-A147

这是一个数学方法，需要推导公式，而不是一个计算机编程可求解的方法（不排除有类似的工具）。根本思想简单来说就是对于一个微分方程，在很难求出其解析解的情况下，可以通过将其参数离散化的方法，譬如以 δx\delta x 为区间分割出一系列的点，求这些点之中的最优解，以求得一个逼近解析解的解。

一般来说，可以按照自变量个数和数据情况进行离散化，离散化越细求得结果越好，但同时求解难度也会上升。

二分搜索

2020-A070

在一些问题中，列出题目所给的所有条件后，因变量相对于自变量的变化趋势是单调的，因而可以进行二分搜索，用较快的时间获取到自变量逼近最优解的解。

有时只能求得一个区间范围，但区间范围规定的区域较小，则可以直接在范围内进行遍历得到最优解。

模拟退火

2020-A070
2020-A212

模拟退火算法最早由 Metropolis 提出，1983 年由 Kirkpatrick 等人将模拟退火的思想成功引入组合优化领域。目前，模拟退火算法已经应用到各门学科中以解决非线性系统的优化问题。

理论上已经证明，模拟退火算法是一个全局最优算法，而且概率 11 接近最优值，并且克服了对初值的依赖。算法的基础源于对固体退火过程的模拟，采用Metropolis 准则，用冷却进度表控制算法进程，最终得到一个近似最优解。固体退火是指将固体加热到足够高的温度后，使分子早随机排列状态，然后逐步降温使之冷却，最后分子以低能状态排列，固体达到某种稳定状态。模拟退火算法的基本思想: 在一定的温度下，搜索从一个状态随机地变化到另一个状态，随着温度的不断下降直到最低温度，搜索过程以概率 1 停留在最优解。根据玻尔兹曼概率分布可以得出:
1.在同一个温度，分子停留在能量较小状态的概率大于停留在能量较大状态的概率。
2.温度越高，不同能量状态对应的概率相差越小;温度足够高时，各状态对应的概率基本相同。
3.随着温度的下降，能量最低状态对应的概率越来越大:温度趋于 0 时，其状态趋于 1。

简单来说，就是在限制空间比较大且没有明显变化趋势，同时也没有一个容易求解的函数（或求解耗时太长）的情况下，选择一种“随机跳”的方式求解。

整体上会有一个“温度”不断降低，然后每次从当前解随机跳一段距离，跳到的位置解如果更优就保留，如果更差就视情况保留（温度越高，保留概率越高，亦即乱跳概率越大），以此不断迭代，达到一定要求后停止求解。

爬山算法

2020-A147

类似于梯度下降。给定一个搜索起点的情况下，在一定临近范围区间内搜索目标函数值最小的点并跳到该点，重复上述过程直到找不到最优点或满足给定最优解条件。

缺陷在于容易陷入局部最优解，可以通过多次运算，每次选取随机初始起点的方式进行一定改善。

A*算法

2020-A147

是一个寻路算法。用于在庞大的解空间中尽可能高速的找到最优解（相比于 Dijkstra 这种需要遍历完整个图的算法而言，A*可能只需要遍历很小的一部分，取决于启发函数的准确性）。

简单来说，对于 Dijkstra 等算法，其目的在于优先搜索从初始点开始的距离 g(x)g(x) 最短的点，而A*算法将其扩展为预计总距离最小的路径上的点，通过设置 f(x)=g(x)+h(x)f(x)=g(x)+h(x) 为比较参数，将其优化到最小。其中 h(x)h(x) 为预估的当前点 xx 到目标点距离，以此估算整条路径距离，再尽可能选择使整条路径更短的新点去进行搜索。

遗传算法

2020-A195
2020-C142

接力进化遗传算法（Relay Evolution Genetic Algorithm）是一种改进的遗传算法（Genetic Algorithm，GA），用于解决多目标优化问题。它通过引入多个种群以及迭代交替的方式来提高算法的性能。

在传统的遗传算法中，只有一个种群进行进化搜索，而接力进化遗传算法使用了多个种群，每个种群都专注于解决不同的子问题或目标。

接力进化遗传算法的基本思想是，在每一代进化过程中，种群之间进行信息共享和传递。具体而言，算法按照顺序为每个种群执行以下步骤：

  1. 选择：从当前种群中选择个体进行繁殖和交叉操作。

  2. 交叉和变异：对所选个体进行交叉和变异操作，生成新的个体。

  3. 竞争：通过竞争选择机制，将新个体与当前种群中的个体进行比较，并保留最好的个体。

  4. 信息传递：选取一部分个体从当前种群传递到下一个种群，成为下一个种群的初始个体。

  5. 迭代：重复以上步骤，直到达到停止条件。

通过这种交替迭代的方式，不同种群之间可以共享优良个体的信息，从而促进全局搜索和多目标优化问题的解决。

接力进化遗传算法在处理多目标优化问题时具有一定的优势，因为它通过将搜索空间分解为多个子问题来提高搜索的效率，并且能够有效地探索和维护多个非支配解集。但是，对于具体问题的适应性和参数选择仍然需要根据实际情况进行调整和优化。

博弈论-纳什均衡

2020-B078
2020-B108
2020-B125

对于有多个参与者参与的博弈论问题，首先需要列出支付矩阵，也就是对于各个参与者的每一种选择在每个情况下的代价大小组成的矩阵，取一种简单情况，两人博弈时局面是对称的，都选 AA 时获利 a0a_0，都选 BB 时获利 b0b_0，分别选 A,BA,B 时分别获利 a1,b1a_1,b_1。则支付矩阵如下：

[(a0,a0)(a1,b1)(b1,a1)(b0,b0)]\left[ \begin{aligned} (a_0,a_0) & & (a_1,b_1) \\ (b_1,a_1) & & (b_0,b_0) \\ \end{aligned} \right]

则设两个玩家选择两个选项的概率分别为 PA,PBP_A, P_B 我们可以通过如下的方式计算该博弈下的纳什平衡点，使得两个玩家的期望收益相等：

PAa0+PBb1=PAa1+PBb0P_A a_0+P_B b_1=P_A a_1 + P_B b_0
PA+PB=1P_A+P_B=1

解方程组即可得到均衡状态下的选择概率。

纯策略纳什均衡和混合策略纳什均衡：在一个博弈论问题中，达到一种纯策略纳什均衡指双方都必定选择某一个选项，此时任何一方改变自己的选项都会让己方收益降低。混合策略纳什均衡指的是，双方都以某一种概率分布进行选择，此时任何一方改变自己的概率分布都将使得自己的收益期望降低，上面计算的期望收益相等的情况就是一种混合策略纳什均衡，当然，上面的方程组也可能计算出其中一个概率大于 11 的情况，此时就不存在一种混合策略纳什均衡。

马尔可夫链

2020-B125
2020-B175

使用马尔可夫链对情况进行建模代表了一种假设：所有的状态转移仅和上一次状态相关。从而根据以往数据计算得出每一个状态向各个状态转移的概率，以此对下一个状态进行概率分布的估计。同时每次到达新状态，也根据新状态情况对估计的概率分布进行更新。

决策树

2020-C109

一种机器学习方法，能够对数据进行分类。
https://zhuanlan.zhihu.com/p/361464944

两种强化方式：将多棵决策树使用加法模型一起训练和使用；加入正则项来减少过拟合。

主成分分析（PCA）

2020-C142

https://zhuanlan.zhihu.com/p/37777074
是一种数据降维算法，能够将高维数据提取特征，映射到一个更低的维度上。具体来说是在原始的空间中顺序找一组相互正交的坐标轴，这些坐标轴选取数据方差最大的方向。

梯度下降

2020-C109

一种求解复杂但可导函数局部最优解的方法。定义一个步长和一个学习率，选取一个初始点，重复以下过程：每次对于当前点，由函数求每个维度上的偏导得到梯度，选取梯度或者梯度的的相反值，将当前点移动步长那么多，然后重复该过程，同时不断降低学习率，直到达到一个局部最优解即梯度为 00 。

有两个缺陷：其一是可能只能到达局部最优解，这一点上不如模拟退火，但是相比模拟退火能更稳定的找到局部最优解，取决于函数运算速度和导数运算速度的差异，速度可能不同。其二是可能卡在鞍点，即梯度为 00 但不是局部最优解，比如三次函数的拐点处。

除了求解梯度，也可以选取某一个或者某几个方向导数进行梯度下降，再进行轮换，分别对应随机梯度下降和小批量梯度下降。使用梯度的梯度下降成为批量梯度下降。

蒙特卡洛模拟

2020-B078

基于随机数的模拟算法，一种应用是求已知函数的概率分布或者积分值。比如给定一个函数 f(x)f(x)，求在 (x1,x2)(x_1,x_2) 范围内的定积分值，已知 f(x)f(x) 的最大最小值，在这个矩形内按单位面积随机选取点，每次选取后计算该点是否在函数包裹的区域内，选取若干点后所求定积分值就是矩形面积乘以点在函数包裹区域内的频率（这里假设矩形不包括因变量为负的部分）。

层次分析法

首先需要决定三个层：目标层、准则层和方案层。目标层就是决策目的，方案层就是所有可选方案，准则则是不同的判断准则，如下图所示：

img

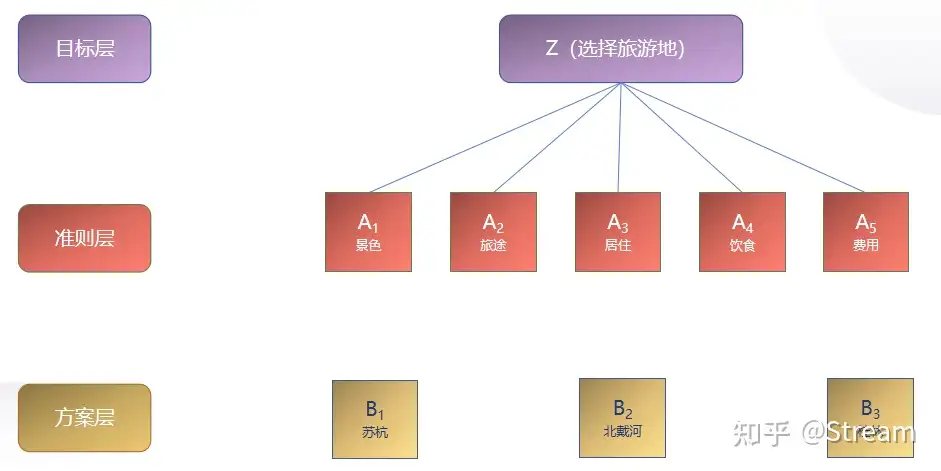
层次分析法是一种在此基础上对各个准则进行排序并最终进行方案选择的分析方法。（可以有多个准则层）

需要构建判断矩阵：

img

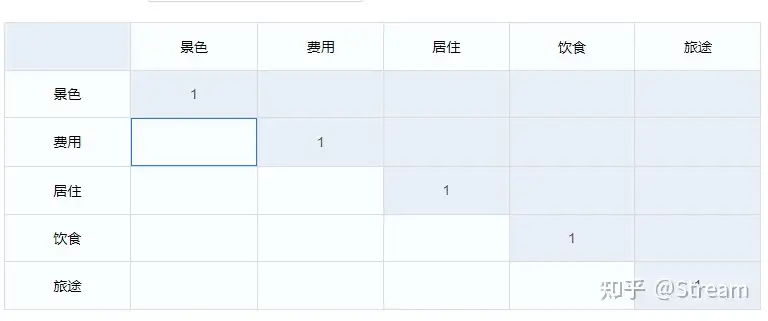
一般根据如下Santy标度方法决定标度：

img

对角线对称的两个位置互为倒数。

然后计算权重向量，一种方法是方根法、一种是和法。共有K个准则时，方根法就是求一行乘积的K次开根，和法则是求每一列归一化之后按行求和。这两种算完之后都需要进行标准化，即算完的各个值应当构成一个K维向量，每一维的值要除以这几维的总和，保证标准化后各维度总和是1。

然后需要进行一些复杂的计算，叫做一致性检验，得出一个CR值，这个值应当小于0.1，否则就说明我们构建判断矩阵的时候出现了逻辑错误，需要对判断矩阵进行修改。

最后得出分析结果。

逻辑回归模型

https://zhuanlan.zhihu.com/p/74874291

逻辑分布：
F(x)=P(X≤x)=11+e−(x−μ)/γ\begin{aligned}F(x)=P(X\le x)=\frac{1}{1+e^{-(x-\mu)/\gamma}}\end{aligned}
f(x)=F′(X≤x)=e−(x−μ)/γγ(1+e−(x−μ)/γ)2\begin{aligned}f(x)=F'(X\le x)=\frac{e^{-(x-\mu)/\gamma}}{\gamma(1+e^{-(x-\mu)/\gamma})^2}\end{aligned}

其中 μ\mu 为位置参数， γ>0\gamma\gt 0 为形状参数。

逻辑回归的本质就是，假设数据服从逻辑分布，然后用极大似然估计做参数的估计。

逻辑回归主要用于分类问题，以二分类为例。

只需要知道可以用来解决二分类或者多分类问题就可以了。

支持

向量机（SVM）

基本想法就是求解能够在给定的一系列高维数据点之中求解能划分数据集并且与两侧的最小几何间距最大的超平面。需要数据集是线性可分的。

需要经过一些复杂的计算，略。
https://www.zhihu.com/tardis/zm/art/31886934?source_id=1005

同时还有非线形SVM算法，可以通过核函数替代内积求解，得到对应的分离超平面。

随机森林

https://zhuanlan.zhihu.com/p/406627649
随机森林的本质是训练若干个决策树，然后对这些决策树的结果取加权平均。随机性的引入使得其不容易过拟合，且有很强的抗噪能力。

比如训练集大小为 NN ，则随机且有放回地从训练集中抽取 NN 个训练样本（即有可能抽取同一个样本多次）作为这棵树的训练集，这导致每棵树的训练集都有所不同。如果存在 MM 个特征，则在每个节点分裂时从其中随机选择 mm 个特征维度来分割节点， mm 保持不变且远小于 MM 。这里每个分类器分类能力越强，森林效果越好。分类器之间相关性越小，森林效果越好。

由于这种分类特征，每棵树都有一部分未被选到的样本称为 OOB (out-of-bag) 样本，使用这些样本输入每个分类器进行分类，用简单多数投票作为分类结果，得到的误差比率就可以作为森林的泛化误差的一个无偏估计，通过比较该值就能获得一个合适的特征数 mm 。

K-近邻（KNN）

一种分类算法。每次对于一个新增的点进行分类时，根据其周围前 KK 个最近的（已经被分类的）邻居的类别决定它的类别。

一般来说会试用不同的 KK 值并最终得到一个使得分类效果最好的值，不同的距离函数也会影响其分类效果。

属于有监督学习。

K-Means

属于无监督学习。

https://zhuanlan.zhihu.com/p/78798251
选择 KK 个随机的点作为聚类中心，对于数据集中的每一个点，根据其距离这 KK 个点中哪一个最近来决定分类到哪一类。分类完成后，对每一个类别的所有点，计算其质心（即各个维度均值位置）作为聚类中心，再重复上述过程，直到达到某个中止条件（迭代次数，最小变化……）

对初始的簇中心敏感，是局部最优，簇近似高斯分布时效果很好，不适合多分类任务，不适合太过离散的分类、样本类别不平衡的分类、非凸形状的分类。

一种优化算法是K-Means++，优化了初始选取的方式：先随机选取一个中心点，再每次计算所有数据到之前所有中心点最远的距离并以一定概率选择，基本就是尽可能选择离之前已选中心点更远的点。

层次聚类

一种分类算法。

https://zhuanlan.zhihu.com/p/54643386
一层一层将所有的样本点逐渐进行一次次合并，得到结果，图片展示起来会比较清晰：

1

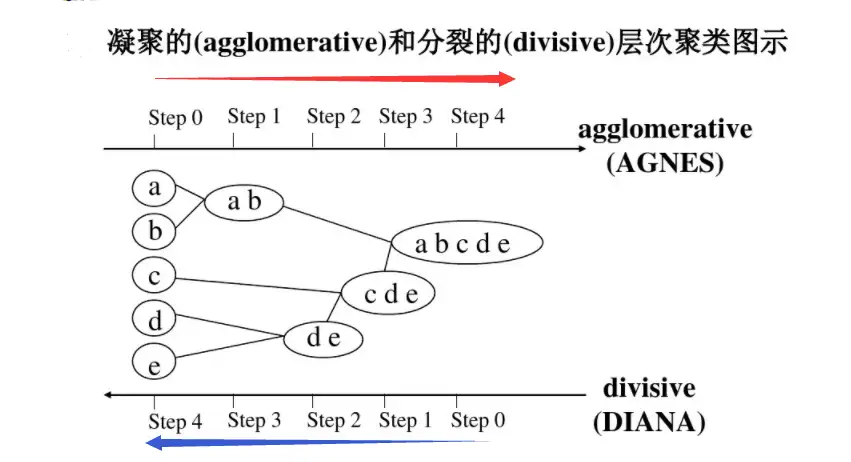
上图的两个方向对应两种算法，AGNES自底向上，初始时每个样本当做一个簇，每次找出距离最近的两个簇将其合并，直到直到最远的两簇距离超过阈值或簇点个数到达指定值。DIANA自顶向下，初始时所有样本在一个簇内，每次对于一个簇，找出其中距离最远的两个点作为两个新簇中心，按剩余点距离哪个近就分到哪个里，不断重复直到最远的两簇距离小于阈值或簇点个数到达指定值。

类似的，度量距离的不同方法也会影响分类结果。

自回归模型（AR）

一种基于历史时间上取值建立回归方程预测未来情况的方式。

https://zhuanlan.zhihu.com/p/435442095
https://zhuanlan.zhihu.com/p/37968357
一个一般建模过程如下：

  1. 首先进行白噪声检验，如果是白噪声不进行建模。
  2. 再进行平稳性检验，如果判定为非平稳，进行平稳化处理后转步骤1，否则进行下一步。
  3. 建立模型，估计参数
  4. 检验适用性，否则重新建模

计算自相关系数（SAF）和偏自相关系数（PACF）后，如果满足下列条件：

  • ACF 具有拖尾性，即 ACF(k) 不会在 k 大于某个常数之后就恒等于 0。
  • PACF 具有截尾性，即 PACF(k) 在 k>p 时变为 0。（用来确定阶数， PACF 在 p 阶延迟后未必严格为 0 ，而是在 0 附近的小范围内波动

则可以尝试使用 AR(k) 模型建模。但还需要进一步确定阶数，可以通过 FPE 准则或贝叶斯信息准则进行确定。

检验模型拟合度可以从两个方面考虑，一个是有效性检验，即残差序列的白噪声检验，再进行显著性检验，简化模型（可以使用T检验）。

滑动平均模型（MR）

类似自回归模型，不过采用一段时间窗口内的均值进行预测。看不懂，// TODO