Jayfeather9's Blog
0%

数学建模国赛算法整理-2

Posted on Edited on In Views:
另一份不完整的简单普通的数学建模国赛算法整理，集中在统计学。

实验设计

正交表

正交试验法是研究多因素多水平的一种设计方法，根据正交性从全面试验中挑选出部分有代表性的点进行试验，这些有代表性的点具备了“均匀分散，齐整可比”的特点，正交试验是分析因式设计的主要方法。也是一种高效率、快速、经济的实验设计方法。它利用一套规格化的表格，即正交表来设计试验方案和分析试验结果，能够在很多的试验条件中，选出少数几个代表性强的试验条件，并通过这几次试验的数据，找到较好的生产条件，即最优的或较优的方案。

正交表获取：https://www.york.ac.uk/depts/maths/tables/orthogonal.htm

PICT

微软开发的自动测试设计命令行工具

共线性问题

https://zhuanlan.zhihu.com/p/355241680

共线性，简单来说就是两个属性之间具有线形的相关关系，比如 y=b0+b1x1+b2x2y=b_0+b_1x_1+b_2x_2，如果 x1,x2x_1,x_2 之间线性相关或者有一定相关程度，分析出来的 b1,b2b_1,b_2 就可以有无穷多种有效的取值，会产生各种各样的问题。后文的大量模型也都是对共线性敏感的，也就是说如果出现了共线性，模型就很容易失效，因此使用一些模型之前最好进行共线性检查。可以通过计算VIF值的大小来判断多重共线性的严重程度，一般来说认为VIF大于10时存在多重共线性。

拟合

高斯过程回归（GPR）

https://zhuanlan.zhihu.com/p/99617693

高斯过程回归是一种回归方式，形式化推导和参考代码可以参考链接，需要定义核函数，常用的包括平方指数核、指核、matern核（常用matern5/2或matern3/2）等。拟合能力较强，同时不仅能够进行预测，也能够给出95%置信度区间，从而得到一个大致的分布。

岭回归和Lasso回归

https://zhuanlan.zhihu.com/p/88698511

是两种对于线性回归的优化，泛化能力更强，以损失部分信息，降低精度为代价让回归系数更符合实际，更可靠，更适用于共线性数据和病态数据。岭回归和Lasso回归分别引入了二范数和一范数作为正则项，同时也可以使得最小二乘中的矩阵一定可逆。

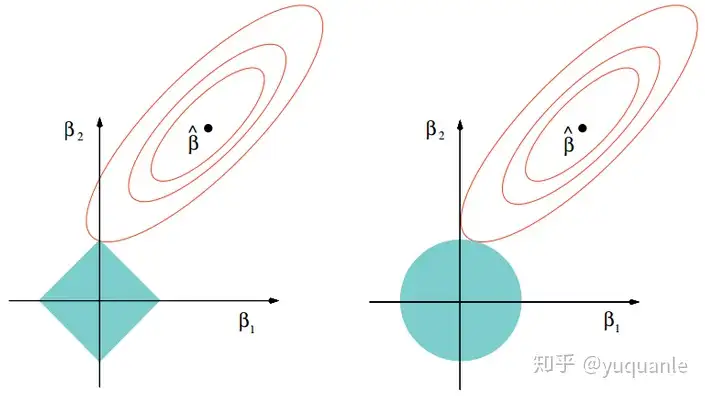
Lasso回归采用一范数来约束，使参数非零个数最少。而Lasso和岭回归的区别很好理解，在优化过程中，最优解为函数等值线与约束空间的交集，正则项可以看作是约束空间。可以看出二范的约束空间是一个球形，一范的约束空间是一个方形，这也就是二范会得到很多参数接近 0 的值，而一范会尽可能非零参数最少。

img

局部加权线性回归

在线性回归基础上为每一个待预测的点引入一个加权的线性模型，根据预测点和数据集中的点的距离给数据集中的点赋予权重，距离预测点更远时权重更小，能够产生一种局部分段拟合的效果，但是因为对每个预测点都要计算与数据集所有点的距离，计算成本较高。（见前面岭回归的链接）

多因素统计分析

https://zhuanlan.zhihu.com/p/362258222
简单来说，就是我们有一堆数据，我们想知道多个维度之间，是否存在这个维度和那个维度有相关性，相关性多大。

可视化可以通过热力图的方式进行。

灰色关联度分析

https://zhuanlan.zhihu.com/p/149479206
需要选定一个母序列，对各个要素进行归一化之后计算关联系数均值，形成关联序。

Pearson 相关系数

可以反映两个连续变量之间的线形相关程度。展示这种相关系数可以将对应的两维数据散点图绘制出来。

Spearman 相关系数

比衡量两个连续变量在排序上的单调关系，与取值无关。如果两个遍变量有非线形的单调关系（递增或者递减），使用 Spearman 相关系数效果会更好。

Kendall 相关系数

https://zhuanlan.zhihu.com/p/33465271

https://zhuanlan.zhihu.com/p/339077538

可以用于离散但有序的变量，如名次、年龄段、肥胖等级等等。也适用于度量两个变量之间的单调关系强弱。有两个计算公式，Tau-a和Tau-b，其中处理有相通值的数据时使用后者。

Uncertainty coefficient（不确定性系数）

用于离散变量和离散变量之间的相关程度。

correlation_ratio

用于连续变量和离散变量的相关程度。

亲和性分析

用于分析一组离散数据中元素与元素之间的亲和度（是否更容易一起出现）。比如有一份商店的购买清单，标注了比如某一单买了芒果苹果香蕉，某一单买了苹果黄油牛奶……

需要计算支持度和置信度。

支持度就是对于某一组物品，这组物品同时出现的交易数 / 交易总数。

置信度就是比如我们要考虑A和B同时出现，那就是AB同时出现在所有包含A的交易的占比。

Apriori

https://zhuanlan.zhihu.com/p/113718432

需要确立一个支持度阈值，然后算法会扫描数据集，不断重复迭代计算，输出满足最小支持度的所有项集，可以经由PCY算法优化内存占用。

卡方检验

https://zhuanlan.zhihu.com/p/551088102
一般用于验证两变量是否相互独立，或者有相关性。

Pearson 卡方检验

要求自由度大于1时，期望次数小于5的字段数不多于总字段的20%。
自由度等于1时，期望次数大于等于10。
自由度：https://zhuanlan.zhihu.com/p/43042410

卡方拟合优度检验

检验一种拟合符合原始数据的程度，在做了回归之后可以使用用以验证结果。

Yates 校正卡方检验

字段期望次数小于5时，不采用Pearson，转而采用Yates。

Fisher 精确检验

样本总量小于40，或某值期望频数小于1，或检验所得P值接近于检验水准α\alpha时采用。

参考：

  • 一般优先考虑皮尔森卡方检验，当 n≥40n\ge 40，T(n)≥5T(n) \ge 5，nn为理论频数，用 Pearson 统计量
  • 当 n≥40n\ge40 时，如果某个格子出现 1≥T≥51\ge T \ge5，则需作叶氏连续性校正
  • 当 n<40n<40，或任何格子出现 T<1T<1，或检验所得的 PP 值接近于检验水准，采用 Fisher 精确检验

分层卡方分析（CMH检验）

在卡方检验基础上考虑混杂因素的分析，比如想要调查某一地区接种疫苗 (X) 对感染病毒 (Y) 的影响，由此来判断疫苗的有效性；但考虑到男性、女性体质的不同，疫苗可能会造成不一样的抵抗病毒能力，因此将性别 (Z) 作为混杂因素来进行分析。

配对卡方检验

配对卡方检验用于分析配对定类变量X1与定类变量X2之间的差异性。它要求数据是配对的，即变量X1、X2是一个事物的同一属性，例如分别采用甲、乙两种方法对同一批病人进行检查，比较此两种方法的结果是否有本质不同，此时要用配对卡方检验。

需要满足：

  • 观测变量是二分类变量（互斥）
  • 分组变量有两类（有三类及以上的用Cochran’s Q检验）

Ridit 分析

用于考察定类变量与有序定类变量之间的差异性。常用于医学研究中，如研究两三种药物对疗效的差异性。其中疗效分为（痊愈、显效、有效、无效），用卡方检验只能反映药物与疗效之间是否有差异，当出现差异性时，无法进一步比较各药物的疗效水平情况。

案例：根据三种药物对于疾病的疗效情况，来分析三种药物的疗效是否有显著差异。本例中以编码的形式给疗效变量的水平进行排序–无效（1）、有效（2）、显效（3）、痊愈（4）。

聚类分析

https://blog.csdn.net/m0_72410588/article/details/130654236
简单来说就是把相似的对象分为一类的算法。

Diriclet回归

可以用来进行多元分类或多标签分类等等任务，总之很强大x

但是没搞懂，先略。

Logistic回归

https://zhuanlan.zhihu.com/p/353112595
是一种分类模型。多重线性回归模型要求因变量是连续型的正态分布变量，且自变量与因变量呈线性关系。当因变量是分类变量，且自变量与因变量不呈线性关系时，就不能确足多重线性回归模型的适用条件。此时，处理该类资料常用Logistic回归模型。Logistic回归分析属于非线性回归，它是研究因变量为二项分类或多项分类结果与某些影响因素之间关系的一种多重回归分析方法。

AdaBoost

一种基于训练多个弱分类器并将其组合得到一个强分类器的，需要一定的数据进行训练。具体来说，初始化时将各个训练样本权值设为相等的值，然后每次训练结束后，对分类效果好的样本降低权值，分类效果不好的样本提高权值，训练下一个弱分类器，如此重复，直到弱分类器个数满足要求，最后按分类器的分类误差大小决定组合时的权重，生成最后用于分类的强分类器。

朴素贝叶斯

https://zhuanlan.zhihu.com/p/26262151

结合先验概率和后验概率，加入了假设：给定目标属性之间相互条件独立，也就是说没有哪个属性变量对决策结果占有较大比重或较小比重。分类效率稳定，适合增量式训练，对缺失数据不敏感，算法简单。但是需要先验概率，要求属性之间不能有太大相关性，存在一定错误率。

当然，各个属性两两之间完全相互独立的情况是相对少见的，因此可以适当放宽假设为“每个属性至多依赖于一个其他属性”即ODE。https://zhuanlan.zhihu.com/p/350772160

取决于如何进行假设，还可以进行细分：如果假设所有属性都依赖于同一个属性，称为“超父”（super-parent），则形成了SPODE算法，如果将每个属性都作为超父构建SPODE，然后集成起来作为最终结果，就形成了AODE算法，是一种基于集成学习机制、更为强大的独依赖分类器。AODE算法需要经过训练。

还有一种改进，通过构建最大带权生成树获得属性之间的依赖关系，这种算法叫做TAN，树增强型贝叶斯算法。https://zhuanlan.zhihu.com/p/377045404，类似的，也会需要训练。

Q型聚类

把所有物体分到不同的簇中，每个物体对应一个簇。

K-Means

无监督、计算简单、速度快、对初始质心敏感，可以使用K-Means++来提升效果。

K-Medoids

随机选取K个样本为中心，将所有样本按距离哪个中心近就划分到哪个簇，在每个簇内，按到簇内所有数据点距离和最小的点作为新的中心，重复直到中心不再变化。

类似K-Means，相比K-Means略慢。

层次聚类

分两种，自底向上或自顶向下，前者对所有分开的物体不断进行合并，后者从包含所有物体的一个簇开始不断将其分裂。

不需要事先确定聚类数目（即K-Means的K），可视化效果好，计算较慢。

DBSCAN

基于密度，能够处理任意形状的簇，能够识别噪声数据，但是对距离度量的选择敏感。

KNN

是一种有监督的算法（需要事先有数据训练），类似K-Means

R型聚类

可能将一个样本分到多个簇。便于了解各个簇之间的亲疏程度，聚类完成后可以选择主要变量进行回归分析或Q型聚类。

可以对所有的变量进行R型分析获得代表性特征变量用于后续分析。

Fuzzy C-Means & Possibilistic C-Means

对噪声数据有较强的容忍性，但是处理高维度系数数据相对困难。

评价类方法

熵权法

https://zhuanlan.zhihu.com/p/267259810根据变异性的大小来确定客观权重，一个指标的信息熵越小，提供的信息量越多。

注意数据要先标准化。

可以根据各个指标的变异程度，给出各个指标的重要性，也就是权重大小，可以用于在不明权重的情况下的赋权的权值决定。

利用主成分分析（PCA）进行评价

计算得到主成分之后，计算各个成分对于主成分的贡献率与累积贡献率，若前几个指标的累积贡献率大于阈值（如85%）则可以说这几个指标主要影响了结果值。

TOPSIS

https://zhuanlan.zhihu.com/p/266689519

逼近理想解排序法。一种充分利用原始数据信息，能够精确地反映各评价方案之间的差距的方法。通过根据各个数据评估方案系统中任何一个方案距离理想最优解和最劣解的距离（通过每个指标都取到系统中的评价指标最优值来决定理想最优方案，最劣方案类似）。

综合距离用这样的表达式衡量：

Sol1−WorstTheoryBest−Worst\begin{aligned}\frac{Sol_1-Worst}{TheoryBest-Worst}\end{aligned}

能够看出，该公式代入最优解值为 11 ，最劣解时为 00 。

但是不同数据取不同类型值时最好，因此要将不同类值进行”正向化处理“。

  • 极大型/极小型指标：越大/小越好，我们的目标是把各类值都转化为极大型。对于极小型，可以选择取负或者取倒数（当所有元素都为正时）
  • 中间型指标：越接近某个目标值越好，则可以取该值和目标值的差值的绝对值：xi^=1−∣xi−xbest∣max{∣xk−xbest∣}\begin{aligned}\hat{x_i}=1-\frac{|x_i-x_{best}|}{max\{|x_k-x_{best}|\}}\end{aligned}
  • 区间型指标：进入某个区间为最好，令 M=max{a−min{xi},max{xi}−b}M=max\{a-min\{x_i\},max\{x_i\}-b\} ，然后进行转化：xi^={1−a−xiM,xi<a1,a<xi<b1−xi−bM,xi>b\hat{x_i}=\left\{\begin{aligned}1-\frac{a-x_i}{M}, && x_i<a \\1,&&a\lt x_i\lt b \\1-\frac{x_i-b}{M},&&x_i\gt b \end{aligned}\right.

然后需要对数据进行标准化：对每个元素，将其改变为：

eS\begin{aligned}\frac{e}{\sqrt{S}}\end{aligned}

其中 ee 为该元素，SS 为该元素所在列的元素平方和，然后就直接取每列的最大、最小值作为最优、最劣解值构成理想最优解和理想最劣解即可，然后计算距离即可得出。

PageRank

https://zhuanlan.zhihu.com/p/137561088

对于图形式的数据，PageRank算法可以对图进行链接分析，是一种无监督学习算法，可以应用于图各个节点的重要度评价问题上。

基本思路就是对于一个有向图，假设一种跳转方式为从任意节点等概率跳转到任何有边连过去的节点，则每一次迭代时，每个节点原本有一个“到这个节点的概率”（马尔可夫链的转移概率），根据跳转方式，将跳转到的目标节点的值用所有跳转过来的节点的原概率乘以跳转概率的求和表示，如此不断迭代直到收敛。

比如三个节点 A,B,CA,B,C 的有向图有边 AB⃗,AA⃗,AC⃗,BA⃗,BC⃗,CA⃗\vec{AB},\vec{AA},\vec{AC},\vec{BA},\vec{BC},\vec{CA}，则可以用如下转移矩阵表示跳转方式：

[13121130013120]\begin{bmatrix}\frac{1}{3} &\frac{1}{2} &1\\ \frac{1}{3}&0&0\\\frac{1}{3}&\frac{1}{2}&0\end{bmatrix}

然后有表示每个节点概率的三维向量 RR，则比如当前时刻的节点概率为 RtR_t，则下一时刻的节点概率 Rt+1=MRtR_{t+1}=MR_t，不断迭代后会收敛到 R=MRR=MR，此时的 RR 就是各个节点的 Pagerank 值。

实际计算中还会为了保证收敛，导入一个平滑项 d∈(0,1)d\in (0,1)，代表每次转移时，有 dd 的概率随机跳转到任意一个节点上，此时能够保证前述的迭代一定收敛。

Box-Behnken-响应面法

https://www.zhihu.com/question/316433312

预测类方法

BP神经网络

BP是反向传播的简写。是一种可以不断“学习”的神经网络，经过数据的训练后能够完成预测工作。

ARMA

自回归滑动平均模型（ARMA）是自回归模型（AR）和滑动平均模型（MA）的混合。

  • 判断时间序列数据是否平稳，不平稳需要做差分处理
  • 判读合适的模型类型并定阶数（AR模型的偏相关函数PACF会P阶截尾，MA模型的自相关函数ACF会Q阶截尾）同时可以通过AIC和BIC准则来判断模型阶数https://zhuanlan.zhihu.com/p/464358562，算出来的AIC和BIC越小越好。

灰色预测

https://zhuanlan.zhihu.com/p/158592530

针对数量非常少（如4个，建议20个以内），数据完整性和可靠性较低的数据进行有效预测，但是只适合于短期预测，其中GM(1,1)使用最为广泛。

建议结合级比值检验，后验差比检验，模型残差检验进行测试。